Yes, math is useful sometimes. And when I say “math” I do not mean simple arithmetic. I mean math. Real math. Calculus, and things like that – such as Fourier transforms.

I learned about FFTs (Fast Fourier Transforms) as an undergrad in university. And today I discovered a use for them in my photography practice. Namely, to remove unwanted repeated patterns from scans of old photos, printed on textured paper.

But let’s start at the beginning. What is a Fourier transform? Well… think about transforming a time-domain picture to a frequency-domain picture. (or, as Wikipedia puts it, “The Fourier transform (FT) decomposes a function (often a function of the time, or a signal) into its constituent frequencies. “. A picture full of repeated lines thus become two dots, for example.

And this (detail from a) picture, full of a repeating pattern due to the original photo paper…:

Becomes this, when transformed through an FFT:

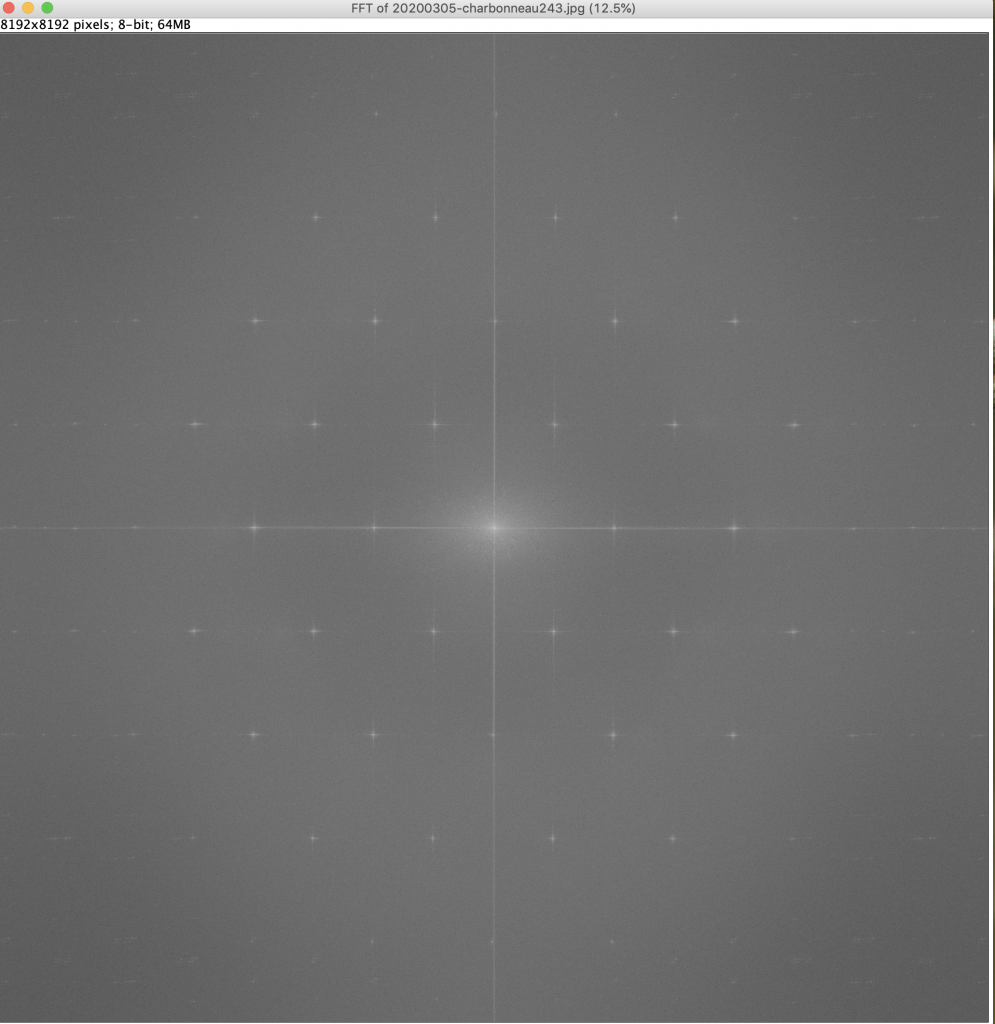
But now I can remove the dots:

..and then I can do a inverse FFT, to end up with this:

And if that isn’t magic, I am not sure what is. There you have it: Magic through math.

Incidentally, the app I use is ImageJ, a free Java-based app from the US National Institutes of Health (NIH). Your tax dollars at work, here: https://imagej.nih.gov/ij/.